And More...First Things First

To illustrate where we are going, here is a sneak preview of a less trivial problem and how it is represented.

The problem is the Eight Queens Problem , a famous puzzle dating back at least to the 19th century. We take it in the form: “Place 8 queens on a chessboard so that no queen is attacking any other.”

Look to the right to see a neat way of representing this problem.

The chessboard is divided one way into “ranks” (horizontal rows) and the other way into “files” (vertical columns), so we say that the ranks and files are the two “Sorts” of thing needed for the problem. Ah, then what about the queens? Well, the important thing about a queen is which square of the board it is on, so as vocabulary for expressing this problem, we introduce the word “queen” as a “function” from files to ranks. For example, “queen(3)” is the (unique) rank where there is a queen on file 3. The “all_different” means that no two queens are allowed to be on the same rank.

The way to read the vocabulary specification is that the word “queen” stands for a function, which expects an argument of sort file and delivers a value of sort rank.

Now, notice that any two queens can be considered as lying at the opposite corners of a rectangle, like this:

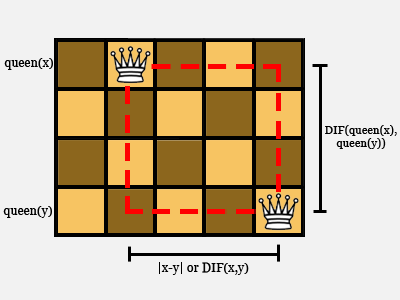
We use the expression “DIF” for the absolute difference (or distance) between two things.

If there are two queens on one diagonal, then their rectangle is a square, meaning the sides are equal. The constraint says this can’t happen (except in the degenerate case where x and y are the same, and their difference is zero).

Click on SOLVE to see the first few solutions.