Using EST: The Queens Again...More Advanced Topics

The best way to understand how “EST” and the other built-ins are used is to look carefully at some examples.

The first example we choose is the N Queens Problem. This is a staple of the literature on constraint satisfaction, as it is easy to state and grasp but not so easy for human beings to solve.

Queens Problem

We are to enumerate the ways of placing n queens on an nxn chessboard in such a way that no queen attacks any other. For the demo, n=8.

Here the placement is represented by a function “queen” which assigns a rank to each file (intuitively, the rank where the queen on that file is placed).

This is a famous (if rather atypical) problem of constraint satisfaction. Logic for Fun does not use a very sophisticated algorithm to solve it, but it does manage to enumerate all the solutions in small cases (up to about n=13) in “reasonable” time. For finding just one solution, local search methods are more effective: specialised solvers can find a solution with millions of queens in a few seconds.

Notice that the problem representation uses two of the built-in functions: “+” allows anything to be incremented by a natural number, and “EST” means “exists”.

This time we are going to formulate it without using the DIF function, but instead using just the built in “+”. As usual, the SOLVER button on the right side of this page has been set to point at a suggested encoding which is worth examining in some detail.

OK, so what does it say? As before, we declare ranks and files as two sorts, and “queen” as an injective function from one to the other. The difference is in the “Constraints” section.

We need to say that the queens do not attack each other along the diagonals, like the two in the image below:

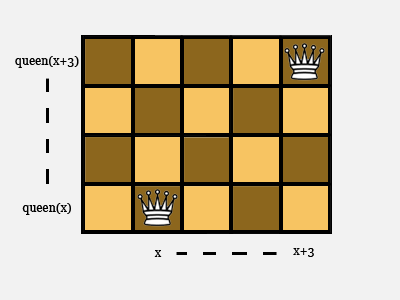
A suitable mathematical description of this scenario is “queen(x+3) = queen(x)+3”. Evidently, what goes for 3 goes for any other number. There is a similar equation recording an attack along the other diagonal, and that’s that!

Well, almost. There are two special cases to take care of. One is where y=0, in which case of course queen(x)+y is the same as queen(x+y). The other is where y is so big that x+y is off the edge of the board. Look at the “Constraints” box to see how these degenerate cases are handled.

How should we read the constraint? It is essentially in two parts, which have been conjoined to avoid repeating the quantifiers and the antecedent of the conditional. If we pick it apart, reformulating it as two constraints, we see that the first half says:

ALL x ALL y ((EST(x+y) AND y > 0) IMP NOT(queen(x)+y = queen(x+y))).

The first literal in this constraint, “EST(x+y)”, is the one that says that x+y is not off the edge of the board. So the whole thing says: “If x+y exists, and is not the same as x, then the queens on files x and x+y are on different diagonals.”

If you hit SOLVE you will see a few solutions, as usual.

Solver

Sorts:

Vocabulary:

Constraints:

Number of solutions:

Time limit:

Pretest limit:

Print finder job:

Print solutions:

Print statistics:

Auto Parser Results

No errors found.